For some states in a Markov chain, there is a positive probability that once the chain transitions out of that state, it will never come back. For instance, in the chain with transition matrix
![\displaystyle \left[ \begin{array}{cc} 0 & 1 \\ 0 & 1 \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+0+%26+1+%5C%5C+0+%26+1+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Once the chain transitions out of state one, it will never again enter state one, as it will stay in state two forever. There are times, however, when the chain will (with probability one) re-enter that state. For example, consider the chain
![\displaystyle \left[ \begin{array}{cc} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+1%2F2+%26+1%2F2+%5C%5C+1%2F2+%26+1%2F2+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
We note that the probability the chain re-enters state one at time  is given by
is given by  as chain must stay in state two for
as chain must stay in state two for  transitions, each of which has probability
transitions, each of which has probability  , and then must finally transition to state one with probability
, and then must finally transition to state one with probability  . Now, the probability the state ever re-enters state one is the union of the events where it first enters at
. Now, the probability the state ever re-enters state one is the union of the events where it first enters at 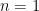 , or at
, or at 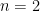 , or
, or 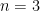 , … These are all disjoint events, though, so we have
, … These are all disjoint events, though, so we have

We say that state  is recurrent if, given
is recurrent if, given  , the probability the chain will ever re-enter state
, the probability the chain will ever re-enter state  is one. If a state is not recurrent, it is called transient. If a state is recurrent, then it will (with probability one) be entered infinitely often, assuming it’s entered at all, as the chain essentially “restarts” itself each time it enters that state, due to the Markov property.
is one. If a state is not recurrent, it is called transient. If a state is recurrent, then it will (with probability one) be entered infinitely often, assuming it’s entered at all, as the chain essentially “restarts” itself each time it enters that state, due to the Markov property.
Now suppose states  and
and  belong to the same class and that state
belong to the same class and that state  is recurrent. Since
is recurrent. Since  and
and  belong to the same class, we have
belong to the same class, we have  . Note that
. Note that 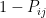 (the probability of not transitioning to state
(the probability of not transitioning to state  from state
from state  ) is less than one. Each time the chain is in state
) is less than one. Each time the chain is in state  there is a chance it will not transition to state
there is a chance it will not transition to state  . However, since
. However, since  is recurrent, it will be entered infinitely often, so the chance of never entering state
is recurrent, it will be entered infinitely often, so the chance of never entering state  is
is

So, if the chain enters state  , it will (with probability one) also enter state
, it will (with probability one) also enter state  at some point. This shows that if
at some point. This shows that if  is recurrent, then
is recurrent, then  must be as well. This shows that recurrence (and transcience) is a class property: in any given class, all states are transient or all states are recurrent.
must be as well. This shows that recurrence (and transcience) is a class property: in any given class, all states are transient or all states are recurrent.
An easier way to test for recurrence is to note that state  is recurrent if and only if
is recurrent if and only if

(This follows by setting 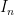 to be the Bernoulli random variable that is one if
to be the Bernoulli random variable that is one if  and zero otherwise. This expected number of times state one is entered is infinite, so
and zero otherwise. This expected number of times state one is entered is infinite, so ![\mathbb{E}\left[\sum I_n \right]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cleft%5B%5Csum+I_n+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) is infinite. By linearity, though, this expectation is simply
is infinite. By linearity, though, this expectation is simply ![\sum \mathbb{E}[I_n] = \sum P_{ii}^{(n)}](https://s0.wp.com/latex.php?latex=%5Csum+%5Cmathbb%7BE%7D%5BI_n%5D+%3D+%5Csum+P_%7Bii%7D%5E%7B%28n%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) .)
.)
Consider the simple random walk where the probability of stepping to the left or right at each transition is 1/2. We will suppose that our states are the integers, like we’re walking along an axis, and that we start in state zero. Note that all states communicate with all other states, so the chain is irreducible (there is only one class of states).
Now, supposing we’re in state zero, what’s the probability we ever re-enter state zero? To enter state zero, we must have had the same number of steps left as right. This is binomially distributed, so the probability that  is
is

Of course, this depends on  being even, so we can rewrite this as
being even, so we can rewrite this as

Using Stirling’s approximation to the factorial, re-writing the above binomial, we have that
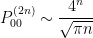
and so summing over all  we have that
we have that  which implies zero is a recurrent state. This in turn implies all states are recurrent.
which implies zero is a recurrent state. This in turn implies all states are recurrent.
transitions is zero unless
is a multiple of some number, say
. If
is the smallest such number, then we say that that state has period
. We’ve already seen an example of a chain with such a state in the simple random walk. In the simple random walk it was impossible to move from any state back to itself in an odd number of transitions: to do so you have to step left the same number of times you step right, which is of course an even number. Since two divides every even number, we have that the state has a period of two. A state with period one is called aperiodic.